CAMBRIDGE IGCSE MATHS (0580)
Paper 2 (P2): Trignometry Topic Quiz 1
Question 1:
Sidney draws the triangle OP1P2.
OP1 = 3 cm and P1P2 = 1 cm.
Angle OP1P2 = 90°.
Sidney draws the triangle OP1P2.
OP1 = 3 cm and P1P2 = 1 cm.
Angle OP1P2 = 90°.
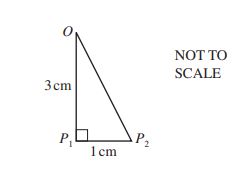
(a) Show that OP2 = √10 cm.
Answer(a) ............................................... [1]
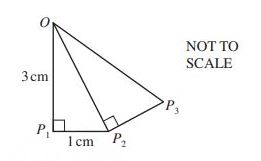
(b) Sidney now draws the lines P2P3 and OP3.
Triangle OP2P3 is mathematically similar to triangle OP1P2.
(i) Write down the length of P2P3 in the form √a/b, where a and b are integers.
Answer(b)(i) P2P3 = ............................................... cm [1]
(ii) Calculate the length of OP3, giving your answer in the form c/d where c and d are integers.
Answer(b)(ii) OP3 = ............................................... cm [2]
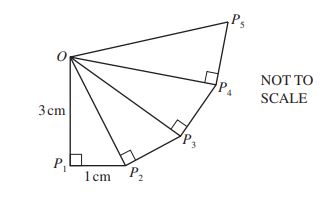
(c) Sidney continues to add mathematically similar triangles to his drawing.
Find the length of OP5.
Answer(c) OP5 = ............................................... cm [2]
(d)
(i) Show that angle P1OP2 = 18.4°, correct to 1 decimal place.
Answer(d)(i) ............................................... [2]
(ii) Write down the size of angle P2OP3.
Answer(d)(ii) Angle P2OP3 = ............................................... [1]
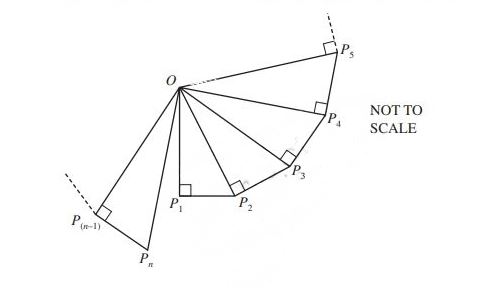
(iii) The last triangle Sidney can draw without covering his first triangle is triangle OP(n–1)Pn.
Calculate the value of n.
Answer(d)(iii) n = ............................................... [3]
Question 2:
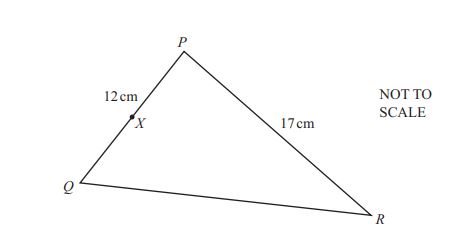
(a) The diagram shows triangle PQR with PQ = 12 cm and PR = 17 cm.
The area of triangle PQR is 97 cm2, and angle QPR is acute.
(i) Calculate angle QPR.
Answer(a)(i) Angle QPR = ................................................ [3]

(a) The diagram shows triangle PQR with PQ = 12 cm and PR = 17 cm.
The area of triangle PQR is 97 cm2, and angle QPR is acute.
(i) Calculate angle QPR.
Answer(a)(i) Angle QPR = ................................................ [3]
(ii) The midpoint of PQ is X. Use the cosine rule to calculate the length of XR.
Answer(a)(ii) XR = .......................................... cm [4]
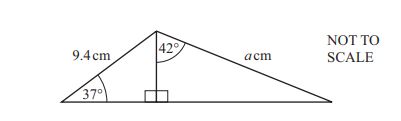
(b) The diagram shows a triangle with angles 37° and 42°, and side 9.4 cm opposite the angle labeled "a".
Calculate the value of a.
Answer(b) a = ................................................ [4]
(c) sin x = cos 40°, 0° ≤ x ≤ 180°. Find the two values of x.
Answer(c) x = .................. or x = .................. [2]
Question 3:
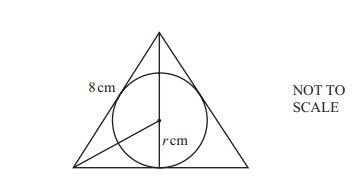
(a) The three sides of an equilateral triangle are tangents to a circle of radius \( r \, \text{cm} \).
The sides of the triangle are 8 cm long.
Calculate the value of \( r \). Show that it rounds to 2.3, correct to 1 decimal place.
Answer(a) ............................................... [3]

(a) The three sides of an equilateral triangle are tangents to a circle of radius \( r \, \text{cm} \).
The sides of the triangle are 8 cm long.
Calculate the value of \( r \). Show that it rounds to 2.3, correct to 1 decimal place.
Answer(a) ............................................... [3]
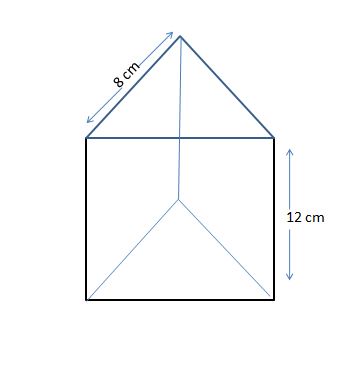
(b) The diagram shows a box in the shape of a triangular prism of height 12 cm.
The cross-section is an equilateral triangle of side 8 cm.
Calculate the volume of the box.
Answer(b) ......................................... cm3 [4]
Question 4:
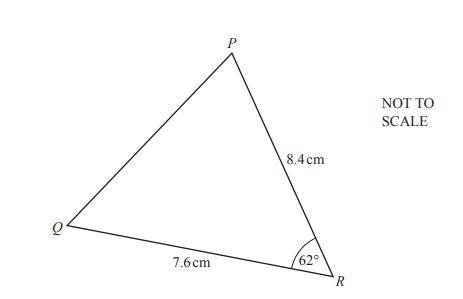
(a) In the triangle PQR, QR = 7.6 cm, PR = 8.4 cm, and angle QRP = 62°.
Calculate:
(i) \( PQ \)
Answer(a)(i) PQ = ........................................... cm [4]
(ii) The area of triangle PQR.
Answer(a)(ii) .......................................... cm2 [2]

(a) In the triangle PQR, QR = 7.6 cm, PR = 8.4 cm, and angle QRP = 62°.
Calculate:
(i) \( PQ \)
Answer(a)(i) PQ = ........................................... cm [4]
(ii) The area of triangle PQR.
Answer(a)(ii) .......................................... cm2 [2]
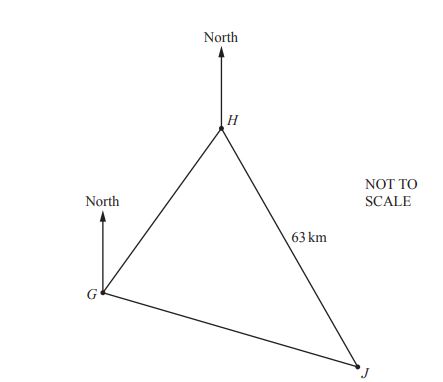
(b) The diagram shows the positions of three small islands G, H, and J.
The bearing of H from G is 045°.
The bearing of J from G is 126°.
The bearing of J from H is 164°.
The distance HJ is 63 km.
Calculate the distance \( GJ \).
Answer(b) GJ = .......................................... km [5]
Question 5:
The diagram shows the positions of two ships, A and B, and a coastguard station, C.
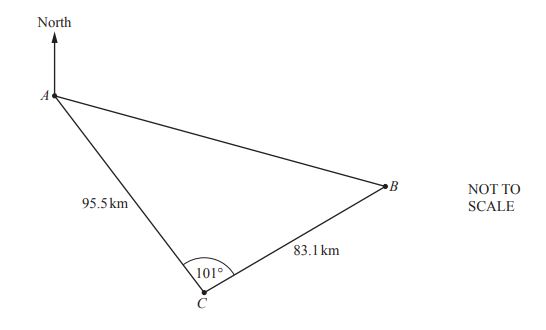
(a) Calculate the distance \( AB \) between the two ships.
Show that it rounds to 138 km, correct to the nearest kilometre.
Answer(a): ................................................ [4]
The diagram shows the positions of two ships, A and B, and a coastguard station, C.

(a) Calculate the distance \( AB \) between the two ships.
Show that it rounds to 138 km, correct to the nearest kilometre.
Answer(a): ................................................ [4]
(b) The bearing of the coastguard station C from ship A is 146°.
Calculate the bearing of ship B from ship A.
Answer(b): ................................................ [4]
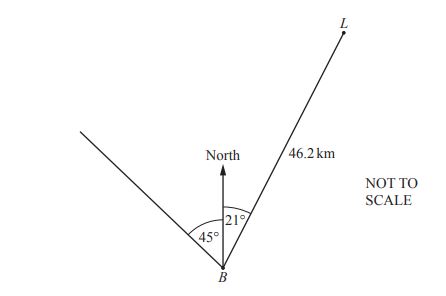
(c) At noon, a lighthouse, \( L \), is 46.2 km from ship B on the bearing 021°.
Ship B sails northwest.
Calculate the distance ship B must sail from its position at noon to be at its closest distance to the lighthouse.
Answer(c): .......................................... km [2]
Question 6:
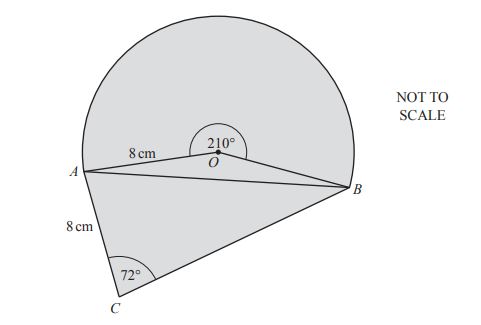
The diagram shows a design for a logo made from a sector and two triangles.
The sector, centre O, has radius 8 cm and sector angle 210°.
AC = 8 cm and angle ACB = 72°.
(a) Show that angle OAB = 15°.
Answer(a): ................................................ [2]

The diagram shows a design for a logo made from a sector and two triangles.
The sector, centre O, has radius 8 cm and sector angle 210°.
AC = 8 cm and angle ACB = 72°.
(a) Show that angle OAB = 15°.
Answer(a): ................................................ [2]
(b) Calculate the length of the straight line AB.
Answer(b): AB = ............................................ cm [4]
(c) Calculate angle ABC.
Answer(c): Angle ABC = ................................................. [3]
(d) Calculate the total area of the logo design.
Answer(d): ............................................ cm2 [6]
(e) The logo design is an enlargement with scale factor 4 of the actual logo.
Calculate the area of the actual logo.
Answer(e): ............................................ cm2 [2]
Question 7:
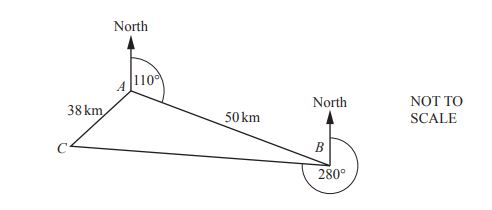

(a) A, B, and C are three towns.
The bearing of B from A is 110°.
The bearing of C from B is 280°.
AC = 38 km and AB = 50 km.
(i) Find the bearing of A from B.
Answer(a)(i): ................................................. [2]


(a) A, B, and C are three towns.
The bearing of B from A is 110°.
The bearing of C from B is 280°.
AC = 38 km and AB = 50 km.
(i) Find the bearing of A from B.
Answer(a)(i): ................................................. [2]
(ii) Calculate angle BAC.
Answer(a)(ii): Angle BAC = ................................................ [5]
(iii) A road is built from A to join the straight road BC.
Calculate the shortest possible length of this new road.
Answer(a)(iii): .......................................... km [3]
Question 8:
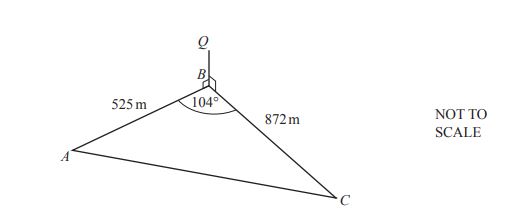
ABC is a triangular field on horizontal ground.
There is a vertical pole BQ at B.
AB = 525 m, BC = 872 m, and angle ABC = 104°.
(a) Use the cosine rule to calculate the distance AC.
Answer(a): AC = ..............................................m [4]

ABC is a triangular field on horizontal ground.
There is a vertical pole BQ at B.
AB = 525 m, BC = 872 m, and angle ABC = 104°.
(a) Use the cosine rule to calculate the distance AC.
Answer(a): AC = ..............................................m [4]
(b) The angle of elevation of Q from C is 1.0°.
Showing all your working, calculate the angle of elevation of Q from A.
Answer(b): ................................................... [4]
(c)
(i) Calculate the area of the field.
Answer(c)(i): ............................................. m2 [2]
(ii) The field is drawn on a map with the scale 1:20,000.
Calculate the area of the field on the map in cm2.
Answer(c)(ii): ............................................ cm2 [2]
Question 9:
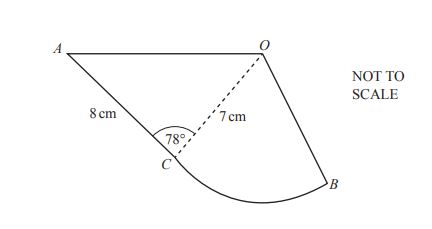
The diagram shows a design made from a triangle AOC joined to a sector OCB.
AC = 8 cm, OB = OC = 7 cm and angle ACO = 78°.
(a) Use the cosine rule to show that OA = 9.47 cm, correct to 2 decimal places.
Answer(a): OA = ........................................ cm [4]

The diagram shows a design made from a triangle AOC joined to a sector OCB.
AC = 8 cm, OB = OC = 7 cm and angle ACO = 78°.
(a) Use the cosine rule to show that OA = 9.47 cm, correct to 2 decimal places.
Answer(a): OA = ........................................ cm [4]
(b) Calculate angle OAC.
Answer(b): Angle OAC = ................................................ [3]
(c) The perimeter of the design is 29.5 cm.
Show that angle COB = 41.2°, correct to 1 decimal place.
Answer(c): Angle COB = ................................................ [5]
(d) Calculate the total area of the design.
Answer(d): ......................................... cm2 [4]
Question 10:
In this question, all measurements are in metres.
2x – 3, x, 6 (NOT TO SCALE)
The diagram shows a right-angled triangle.
In this question, all measurements are in metres.
2x – 3, x, 6 (NOT TO SCALE)
The diagram shows a right-angled triangle.
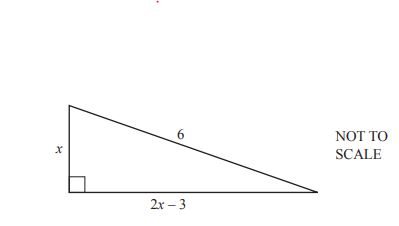
(a) Show that 5x2 – 12x – 27 = 0.
Answer(a): ....................................................... [3]
(b) Solve 5x2 – 12x – 27 = 0.
Show all your working and give your answers correct to 2 decimal places.
Answer(b): x = ......................... or x = ......................... [4]
(c) Calculate the perimeter of the triangle.
Answer(c): ............................................ m [2]
(d) Calculate the smallest angle of the triangle.
Answer(d): ................................................. [2]
Question 11:
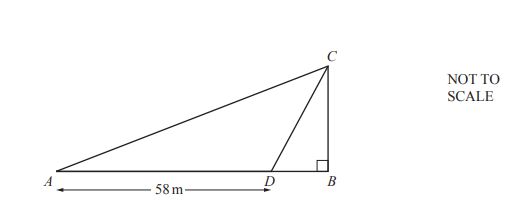
(a)
In the diagram, BC is a vertical wall standing on horizontal ground AB.
D is the point on AB where AD = 58 m.
The angle of elevation of C from A is 26°.
The angle of elevation of C from D is 72°.

(a)
In the diagram, BC is a vertical wall standing on horizontal ground AB.
D is the point on AB where AD = 58 m.
The angle of elevation of C from A is 26°.
The angle of elevation of C from D is 72°.
(i) Show that AC = 76.7 m, correct to 1 decimal place.
Answer(a)(i): ....................................................... [5]
(ii) Calculate BD.
Answer(a)(ii): BD = .......................................... m [3]
(b) Triangle EFG has an area of 70 m².
EF : FG = 1 : 2 and angle EFG = 40°.
(i) Calculate EF.
EF = .......................................... m [4]
(ii) A different triangle PQR also has an area of 70 m².
PQ : QR = 1 : 2 and PQ = EF.
Find angle PQR.
Angle PQR = .............................................. [1]
Solution

