CAMBRIDGE IGCSE MATHS (0580)

Question 1:
(a) The diagram shows two sets of cards:

(i) Jojo chooses two cards at random from Set A without replacement.
Find the probability that the two cards have the same number.
................................................ [3]

(ii) Jojo replaces the two cards. Kylie then chooses one card at random
from Set A and one card at random from Set B.
Find the probability that the two cards have the same number.
................................................ [3]

(iii) Who is the most likely to choose two cards that have the same number?
Show all your working.
................................................ [1]

(b)

Lena chooses three cards at random from Set C without replacement.
Find the probability that the third card chosen is numbered 4.

Question 2:
The probability that Andrei cycles to school is r.
(a) Write down, in terms of r, the probability that Andrei does not cycle to school.
............................................... [1]

(b) The probability that Benoit does not cycle to school is 1.3 - r.
The probability that both Andrei and Benoit do not cycle to school is 0.4.
(i) Complete the equation in terms of r.
() # () = 0.4 [1]

(ii) Show that this equation simplifies to
10r² - 23r + 9 = 0.
............................................... [3]

(iii) Solve by factorisation
10r² - 23r + 9 = 0.
r = or r = [3]

(iv) Find the probability that Benoit does not cycle to school.
............................................... [1]

Question 3:
(a) Angelo has a bag containing 3 white counters and x black counters.
He takes two counters at random from the bag, without replacement.
(i) Complete the following statement:
The probability that Angelo takes two black counters is \[ \frac{x}{x+3} \times \_\_\_\_\_\_ \] [2]

(ii) The probability that Angelo takes two black counters is \[ \frac{7}{15}. \]
(a) Show that: \[ 4x^2 - 25x - 21 = 0. \] [4]

(b) Solve by factorisation:
\[ 4x^2 - 25x - 21 = 0 \]
x = or x = [3]

(c) Write down the number of black counters in the bag.
............................................... [1]

(b) Esme has a bag with 5 green counters and 4 red counters.
She takes three counters at random from the bag, without replacement.
Work out the probability that the three counters are all the same colour.
............................................... [4]

Question 4:
Kenwyn plays a board game. Two cubes (dice) each have faces numbered 1, 2, 3, 4, 5, and 6.
In the game, a throw is rolling the two fair 6-sided dice and then adding the numbers on their top faces.
This total is the number of spaces to move on the board.
For example, if the numbers are 4 and 3, he moves 7 spaces.

(a) Giving each of your answers as a fraction in its simplest form, find the probability that he moves:
(i) two spaces with his next throw.
................................................ [2]

(ii) ten spaces with his next throw.
................................................ [3]

(b) What is the most likely number of spaces that Kenwyn will move with his next throw?
Explain your answer.
................................................
Because ................................................ [2]

(c)

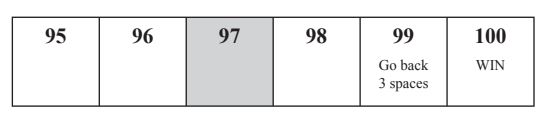
To win the game, he must move exactly to the 100th space. Kenwyn is on the 97th space.
If his next throw takes him to 99, he has to move back to 96.
If his next throw takes him over 100, he stays on 97.
Find the probability that he reaches 100 in either of his next two throws.
................................................ [5]

Question 5:
(a) A bag contains red beads and green beads. There are 80 beads altogether.
The probability that a bead chosen at random is green is 0.35.

(i) Find the number of red beads in the bag.
................................................. [2]

(ii) Marcos chooses a bead at random and replaces it in the bag.
He does this 240 times.
Find the number of times he would expect to choose a green bead.
................................................. [1]

(b) A different bag contains 2 blue marbles, 3 yellow marbles, and 4 white marbles.
Huma chooses a marble at random, notes the colour, then replaces it in the bag.
She does this three times.

(i) Find the probability that all three marbles are yellow.
................................................. [2]

(ii) Find the probability that all three marbles are different colours.
................................................. [3]

(c) Another bag contains 2 green counters and 3 pink counters.
Teresa chooses three counters at random without replacement.
Find the probability that she chooses more pink counters than green counters.
................................................. [4]

Question 6:
A box contains 20 packets of potato chips.
6 packets contain barbecue flavoured chips.
10 packets contain salt flavoured chips.
4 packets contain chicken flavoured chips.

(a) Maria takes two packets at random without replacement.
(i) Show that the probability that she takes two packets of salt flavoured chips is \( \frac{9}{38} \).
[2]

(ii) Find the probability that she takes two packets of different flavoured chips.
................................................. [4]

(b) Maria takes three packets at random, without replacement, from the 20 packets.
Find the probability that she takes at least two packets of chicken flavoured chips.
................................................. [3]

Question 7:


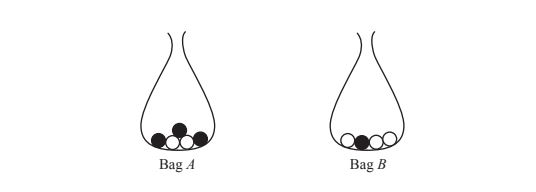
Bag A contains 3 black balls and 2 white balls.
Bag B contains 1 black ball and 3 white balls.

(a) A ball is taken at random from each bag.
(i) Show that a black ball is more likely to be taken from bag A than from bag B.
[1]

(ii) Find the probability that the two balls have different colours.
.................................................. [3]

(b) The balls are returned to their original bags.
Three balls are taken at random from bag A, without replacement.
Find the probability that
(i) they are all black,
.................................................. [2]

(ii) they are all white.
.................................................. [1]

(c) The balls are returned to their original bags.
A ball is taken at random from bag A and its colour is recorded.
This ball is then placed in bag B.
A ball is then taken at random from bag B.
Find the probability that the ball taken from bag B has a different colour
to the ball taken from bag A.
.................................................. [3]